

Next: Minimum-controlled recursive averaging noise
Up: Speech Enhancement Summaries
Previous: Frequency to eigendomain transform
Let
![$y[n]=x[n]+b[n]$](img21.png) and
and
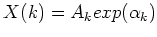 with the noise having a Gaussian distribution.
The prior density function is (also see Ephraim and Malah suppression rule):
with the noise having a Gaussian distribution.
The prior density function is (also see Ephraim and Malah suppression rule):
The maximum-likelihood approach attempts to choose the parameter value that maximizes the parameterized pdf, that is the parameter value which is most likely to have caused the observation.
The ML estimation is used for estimating an unknown parameter of a given pdf when no a priori information about it is available.
The performance of the algorithm during silent frames is not adequate because the starting assumption is that the signal is always present.
The authors suggest a two-state soft-decision approach by using the binary hypothesis model:
The MMSE solution is
since
![$\mathcal{E}[A_k\vert Y_k,H_1]$](img44.png) is the minimum variance estimate of A and the Maximum Likelihood estimate is asymptotically efficient.
is the minimum variance estimate of A and the Maximum Likelihood estimate is asymptotically efficient.
Assuming
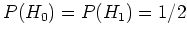 and using Bayes' theorem,
and using Bayes' theorem,
denoting
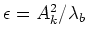 to be the a priori SNR and
to be the a priori SNR and
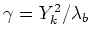 to be the a posteriori SNR.
to be the a posteriori SNR.


Next: Minimum-controlled recursive averaging noise
Up: Speech Enhancement Summaries
Previous: Frequency to eigendomain transform
Vinesh Bhunjun
2004-09-17
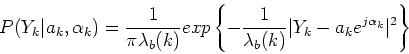
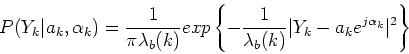
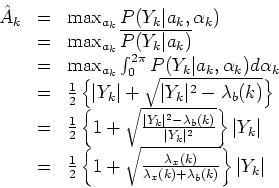

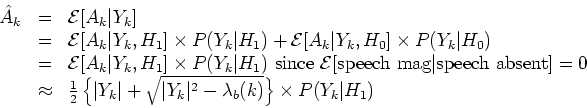
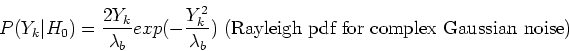
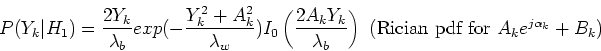
![\begin{displaymath}
P(Y_k\vert H_1)=
\frac
{exp(-\epsilon)I_0\left[2\sqrt{\ep...
...]}
{1+exp(-\epsilon)I_0\left[2\sqrt{\epsilon \gamma}\right]}
\end{displaymath}](img48.png)