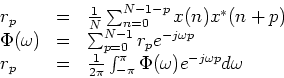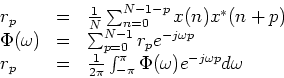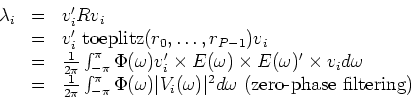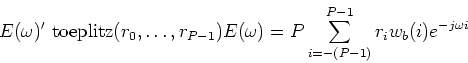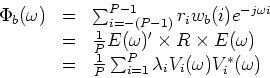

Next: Maximum-Likelihood spectral amplitude estimator [6]
Up: Speech Enhancement Summaries
Previous: Ephraim and Malah suppression
Denote
![$E(\omega)=[1 \quad e^{-j\omega} \quad \ldots \quad
e^{-j\omega (P-1)}]'$](img32.png) Given the covariance matrix
Given the covariance matrix
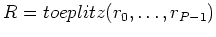 where
where
Form
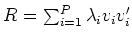 . The Frequency to
Eigendomain Transformation is given by
. The Frequency to
Eigendomain Transformation is given by
To find the Inverse Frequency to Eigendomain Transformation
consider
where 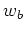 is the Bartlett (triangular) window.
is the Bartlett (triangular) window.
Vinesh Bhunjun
2004-09-17