

Next: Bayes optimal decision rule
Up: Speech Enhancement Summaries
Previous: Bark filter approach[10]
Define a risk (or average/expected cost)
The Bayes estimate minimizes the risk with respect to 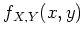 , the joint probability density function of
, the joint probability density function of 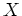 and
and 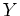 .
As
.
As 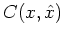 is non-negative, it is sufficient to minimize only the inner integral, giving
is non-negative, it is sufficient to minimize only the inner integral, giving
The optimal solution in the Minimum Mean Square Error sense is given by the mean of the posterior density, i.e. the conditional mean
![$\mathcal{E}[X\vert Y]$](img12.png) of r.v.
of r.v. 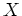 given r.v.
given r.v. 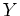 is the MMSE estimate of
is the MMSE estimate of 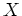 given
given 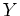 .
.
Vinesh Bhunjun
2004-09-17
![\begin{displaymath}
\begin{array}{lll}
\mathcal{R}&=&\mathcal{E}[C(x,\hat{x})]...
...ty} C(x,\hat{x}) f_{X\vert Y}(x\vert y) dx dy\\
\end{array}
\end{displaymath}](img6.png)
![\begin{displaymath}
\begin{array}{lll}
\mathcal{R}&=&\mathcal{E}[C(x,\hat{x})]...
...ty} C(x,\hat{x}) f_{X\vert Y}(x\vert y) dx dy\\
\end{array}
\end{displaymath}](img6.png)
![]() of r.v.
of r.v. ![]() given r.v.
given r.v. ![]() is the MMSE estimate of
is the MMSE estimate of ![]() given
given ![]() .
.
![\begin{displaymath}
\begin{array}{lll}
\mathcal{E}[(X-f(Y))^2] & = & \mathcal{...
...ge & \mathcal{E}[(X-\mathcal{E}[X\vert Y])^2]\\
\end{array}
\end{displaymath}](img13.png)