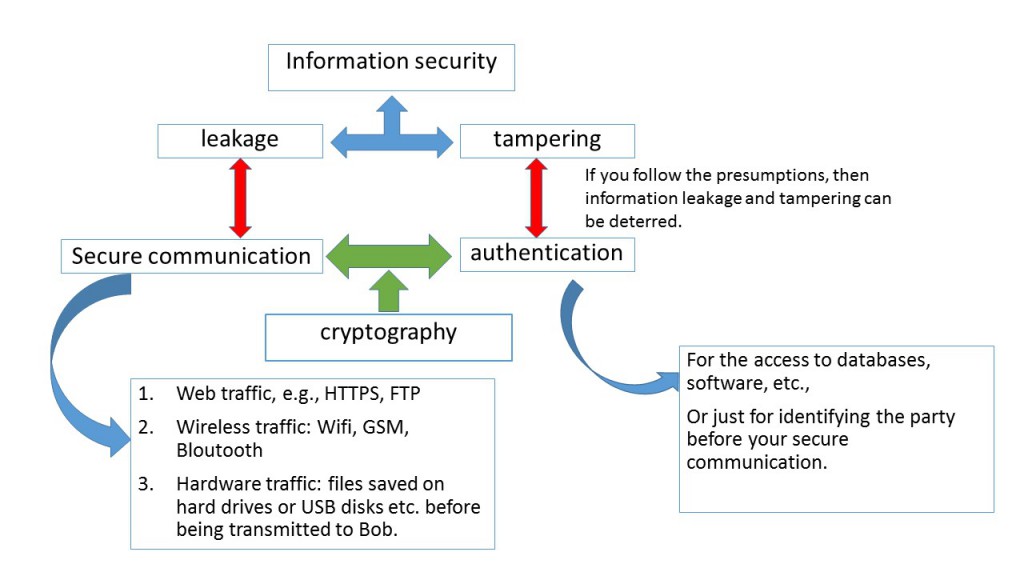
In this exposition, we want to emphasize the approximate message passing (AMP) has superior complexity when serving Massive MIMO uplink detection problems, although AMP was initially proposed for solving LASSO [DMM09]. Regarding expository details about why AMP works, please see [BM11].
Now we share simulation results as well as MATLAB source codes.
% AMP detector in Massive MIMO
% written by Shanxiang Lyu (s.lyu14@imperial.ac.uk)
% Last updated on 04/12/2015
function main()
clc;clear; close all;
m=128;% # of received antennas
n=16;% # of users
SNRrange=[1:20];
count=0;
for s=SNRrange
SNRdb=s;
for monte=1:1000
x=(2*randi([0,1],n,1)-ones(n,1))+sqrt(-1)*(2*randi([0,1],n,1)-ones(n,1));
sigmas2=2;%signal variance in QPSK
H=1/sqrt(2*m)*randn(m,n)+sqrt(-1)/sqrt(2*m)*randn(m,n);
sigma2=2*n/m*10^(-SNRdb/10); %noise variance in control by SNR in DB
w=sqrt(2*sigma2)*randn(m,1)+sqrt(-1)*sqrt(2*sigma2)*randn(m,1);
y=H*x+w; %channel model
%iterAMP is # of iterations in AMP
iterAMP1=2;
xhat1=AMP(y,H,sigma2,sigmas2,iterAMP1,m,n);
iterAMP2=4;
xhat2=AMP(y,H,sigma2,sigmas2,iterAMP2,m,n);
x_mmse=(sigma2/sigmas2*eye(n)+H'*H)^(-1)*H'*y;
x_mmse=sign(real(x_mmse))+sqrt(-1)*sign(imag(x_mmse));
errorAMP1(monte)=sum(x~=xhat1);
errorAMP2(monte)=sum(x~=xhat2);
errorMMSE(monte)=sum(x~=x_mmse);
end
count=count+1;
serAMP1(count)=mean(errorAMP1);
serAMP2(count)=mean(errorAMP2);
serMMSE(count)=mean(errorMMSE);
end
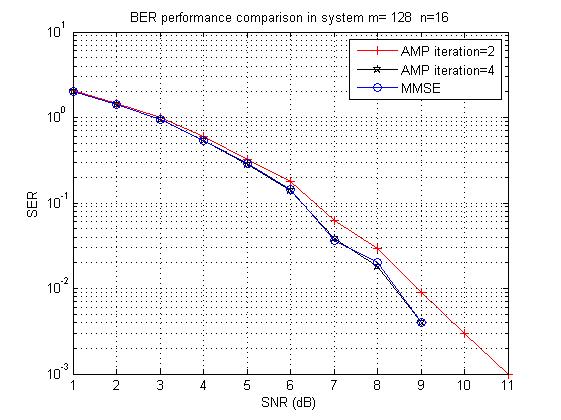
figure(1)% plot the SER
semilogy(SNRrange,serAMP1,'-+r', SNRrange,serAMP2,'-pk',SNRrange, serMMSE,'-ob');
grid on;
legend(['AMP iteration=' int2str(iterAMP1)], ['AMP iteration=' int2str(iterAMP2)], 'MMSE');
xlabel('SNR (dB)'); ylabel('SER');
title(['BER performance comparison in system m= ' int2str(m) ' n=' int2str(n)]);
end
function xhat=AMP(y,H,sigma2,sigmas2,iterAMP,m,n)
% AMP detector in Massive MIMO
% written by Shanxiang Lyu (s.lyu14@imperial.ac.uk)
% Last updated on 04/12/2015
r=zeros(m,1);
xhat=zeros(n,1);
alpha=sigmas2;%initial estimation variance
for t=1:iterAMP
r=y-H*xhat+(n/m)*sigmas2/(sigmas2+alpha)*r;
alpha=sigma2+(n/m)*sigmas2*alpha/(sigmas2+alpha);
xhat=(sigmas2/(sigmas2+alpha))*(H'*r+xhat);
end
xhat=sign(real(xhat))+sqrt(-1)*sign(imag(xhat));
end