Research Progress Report *
on Directional Image Representations
Summary of 1st year of research from
November 2003 to October 2004,
carried out by Mr. Pancham Shukla under the supervision of Dr P L Dragotti
Communications and Signal
Processing Research Group
Department of Electrical
and Electronic Engineering
1.
Introduction
According to
In recent past, Unser et al. extended the conventional ‘bandlimited-sinc’ scenario to classes of signals such as uniform Splines, which are not bandlimited but reside in a subspace spanned by a generating function and its shifted versions [1,2]. Very recently, Vetterli et al. showed that it is possible to develop sampling schemes for a larger class of signals that are neither bandlimited nor reside in a vector subspace but subsist in a nonlinear space of finite dimension. Such signals are classified as signals with Finite Rate of Innovation (FRI). Streams of Diracs and piecewise polynomial signals are the examples of such signals. Vetterli et al. addressed the sampling of FRI signals using Sinc and Gaussian kernels in Fourier domain [3,4].
For many natural images, often, the region of interest may be reasonably modelled with the FRI structures, and these structures may follow random distributions and orientations. Following the above hypothesis, our objective is to investigate how efficiently we can sample and reconstruct the set of FRI signals from only a few samples employing a more general set of sampling kernels that can closely match the characteristics of acquisition devices. For 1-D signals, Dragotti et al. showed that wavelets can be an effective choice as sampling kernel [5]. This may be attributed to its improved time-frequency localization and compact support. Initial results on wavelet sampling of 1-D FRI signals are promising but the problem becomes more involved for the multidimensional case as usual. In the first phase of our research, we are addressing wavelet sampling and reconstruction of 2-D FRI structures, in particular, streams of Diracs and piecewise constants (planar polygons).
2.
Materials and Methods
Sampling
setup
We use a 2-D generic sampling
setup as shown in Figure 1, where the 2-D FRI signal 
to be sampled is filtered with smoothing kernel 
and a uniform set of samples 
is available from the
filtered version 
with the inner product:
where 
are sampling intervals
in 
and 
directions respectively over a uniform rectangular lattice.
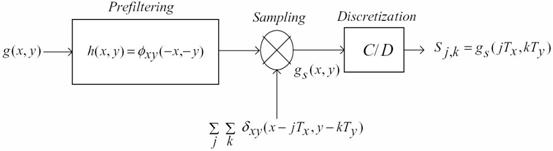
Figure 1: 2-D generic sampling setup.
FRI signals
The signal is composed of some
simple FRI structures such as streams of 2-D Diracs and planar polygons (piecewise
constants). For simplicity, the planar polygons can be classified in two
classes; parallel boundary and skewed boundary depending on the orientation
(angle) complexity of the boundaries. The selected FRI structures are depicted
in Figure 2.
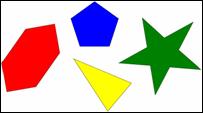
Figure 2:
(a) left: streams of Diracs, (b) centre: parallel boundary polygons, (c) right:
skewed boundary polygons.
Sampling
kernel
The selected sampling kernel is a
compactly supported 2-D separable scaling function 
obtained from any
valid 1-D scaling function 
. For example, 2-D Linear Spline and Daubechies sampling
kernels are shown in Figure 3.
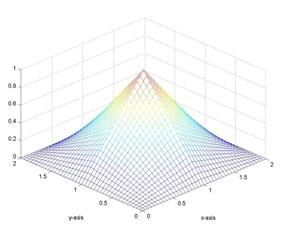
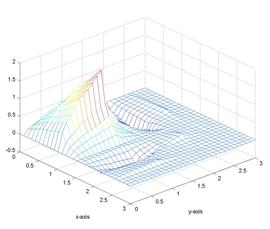
Figure 3: (a) left: liner Spline kernel (b) right: 4-tap Daubechies kernel.
Important
properties of sampling kernel
At the heart of the research reclines
the partition of unity and polynomial approximation properties of the sampling
kernel 
as highlighted in
Figure 4. These crucial properties of the kernel play a major role in sampling
and reconstruction of the selected classes of FRI structures.
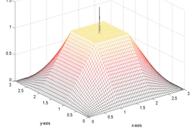
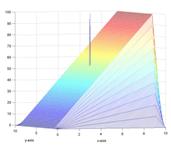
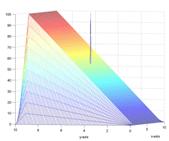
Figure 4: (a)
left: partition of unity, responsible for reconstruction of the amplitude of
the Dirac, (b) centre: reproduction of polynomial of degree 1 in direction, responsible for locating the-coordinate of the Dirac (c) right: reproduction of
polynomial of degree 1 in direction, responsible for locating the-coordinate of the Dirac.
Related tools and techniques
We also adopt the following techniques in order to generalize our algorithms in reconstructing the FRI structures from their finite number of samples.
1. Annihilating filter methods [3]: We use them for the cases of densely packed Diracs and for locating (and reconstructing) the complex-valued vertices of planar polygons (in particular, skewed boundary ones) from their complex-valued moments [7,9].
2. Radon transform projections [6,7]: A close connection between the moment property (line integrals) of radon projections and partition of unity of wavelet sampling kernel is exploited in determining the orientations of the boundaries of planar polygons.
3. Directional derivatives [8]: This procedure facilitates to decompose the problem of sampling a range of planar polygons into a generalized formulation of sampling the streams of Diracs with any valid sampling kernel. It leads to a local and less complex solution for reconstruction of planar polygons with the significant flexibility in the orientation of their boundaries.
4. Complex moments [7,9]: This approach provides a global solution for the reconstruction of planar polygons (in particular, skewed boundary ones) form their complex-valued moments. However, it poses concerns on the complexity and stability in reconstruction for the polygons with many vertices.
3.
Results and future work
We have
extended several ideas of continuous domain to our discrete setup, i.e. a set
of a finite number of samples. The properties shown in Figure 4, and the directional
derivatives along the sampling axis allowed us to sample and reconstruct simple
cases of FRI structures such as a single Dirac per area and parallel boundary
polygons. The promising results encouraged us to generalize our model for more
complex cases, i.e. more number of Diracs per area and skewed boundary
polygons.
By discovering the relevant connections
of the related tools and techniques (as mentioned above) to our wavelet
sampling, we are successful in sampling and reconstructing the streams of 2-D
Diracs and planar polygons with different structural complexities (more than
one Diracs per area, and a large range of permissible orientations for the
boundaries of planar polygons). For both types of FRI structures, we have
derived a couple of novel algorithms that can be employed locally or globally
depending on the structural complexity of a given FRI signal. Finally, we
should accentuate that our implementation allows a wide choice of wavelets as
sampling kernel and requires only a finite number of samples for reconstruction
algorithms. This has a direct practical relevance in the design of acquisition
devices and processing algorithms for the state-of-the-art digital cameras.
We are currently working on extending the notion of wavelet footprints (a multiresolution framework for resolution enhancement [10]) in 2-D by incorporating our sampling results on FRI structures. Efficient ways of presenting 2-D directional structures with footprints should improve the performance of many commercial applications. We anticipate that the future work might offer some novel schemes to the current state of image-resolution enhancement (or super-resolution imaging).
The image-resolution enhancement has many applications such as, the corner point detection in blurred satellite images, position detection in robotics and machine vision, and diagnostics in bio-medical imaging. To judge the current and future potential of this subject, we refer to the issue of IEEE Signal Processing Magazine [11].
References
[1].
M Unser. Sampling- 50 Years after
[2].
A Aldroubi and K Grochenig. Non-uniform
sampling in shift-invariant spaces.
[3].
Martin Vetterli, Pina Marziliano, and Thierry Blu. Sampling signals with finite
rate of innovation. IEEE Transactions on Signal Processing, 50(6):1417-1428.
June 2002.
[4]
Irena Maravic and Marin Vetterli. Exact sampling results for some classes of
parametric nonbandlimited 2-D signals. IEEE Transactions on Signal Processing,
52(1):175-189, January 2004.
[5].
P L Dragotti and M Vetterli. Wavelet and footprint sampling of signals with a
finite rate of innovation. In Proceedings of IEEE International conference on
Acoustics, Speech and Signal Processing (ICASSP),
[6].
I Maravic and M Vetterli. A sampling theorem for the Radon transform of finite
complexity objects. In Proceedings of
IEEE International Conference on Acoustics, Speech and Signal Processing
(ICASSP),
[7].
P Milanfar, G Verghese, W Karl , and A Willsky. Reconstructing polygons from
moments with connections to array processing. IEEE Transactions on Signal
Processing, 43:432-443, February 1995.
[8].
V Velisavljevic, B Beferull-Lozano, M Vetterli and P L Dragotti. Discrete
multi-directional wavelet bases, In Proceedings of IEEE International
Conference on Image Processing (ICIP),
[9].
M Elad, P Milanfar, and G H Golub. Shape from moments- an estimation theory
perspective. IEEE Transactions on Signal Processing, 52(7):1814-1829, July
2004.
[10].
P L Dragotti and M Vetterli. Wavelet
footprints: theory, algorithms and applications, IEEE Transactions on
Signal Processing, 51(5):1306-1323, May 2003.
[11].
-----, IEEE Signal Processing Magazine, 20(3), May 2003.
* The time scale of the first year research is illustrated through the attached Gant chart.